Expérimentation “Les Noums CP”, démarche théorique et pratique

Ci-dessous un résumé de l’article écrit par Rémi Brissiaud sur le site www.cafepedagogique.com

On peut lire dans les dernières préconisations ministérielles : “Introduire des représentations, sous forme de schémas bien adaptés, permettant la modélisation des problèmes proposés“. L’origine de la recommandation ministérielle d’utiliser des schémas conventionnels pour résoudre les problèmes arithmétiques n’est pas très difficile à trouver : c’est ce qui est fait dans la méthode de Singapour. Cependant, en recommandant leur usage dès le CP, le texte ministériel sous-estime la complexité de l’activité de modélisation à l’aide des schémas conventionnels utilisés par la méthode de Singapour.

Chez les élèves qui rencontrent des difficultés avec les nombres, on note parfois une régression des performances.

Cela s’explique aisément : la méthodologie enseignée aux élèves consiste à choisir le bon schéma avant d’y placer les valeurs numérique et d’écrire l’égalité (situation de type Parties-Tout, de type Transformation positive, de type Comparaison, …?)

Se livrer à une telle analyse sémantique de l’énoncé est loin d’être facile. On peut même considérer que la recherche du bon schéma fait, chez eux, obstacle à la compréhension du texte. Ils ne se demandent plus « De quoi parle cet énoncé ? », ils ne cherchent plus à simuler mentalement la situation décrite, ils sont à la recherche d’indices permettant d’apparier l’énoncé à l’un des schémas.

Or, on sait aujourd’hui (Brissiaud & Sander, 2010 ; Thevenot & Barrouillet, 2015) que toute résolution de problèmes commence par une simulation mentale de la situation décrite dans l’énoncé. Tout ce qui risque de détourner l’enfant de cette étape nécessaire est susceptible de faire obstacle au progrès.

Quelle(s) solution(s) ?

-Enseigner les propriétés conceptuelles des opérations via le calcul mental, pour ensuite s’engager vers la résolution de problèmes.

-Renoncer provisoirement à l’usage du “bon schéma” afin de s’appuyer de manière privilégiée sur les schématisations spontanées des élèves pour ensuite les amener à passer du dessin au schéma conventionnel. Il ne faut pas pour autant renoncer à tout usage précoce de schémas conventionnel.

-Disposer d’un environnement pédagogique permettant aux élèves de ne pas se livrer d’emblée à une analyse sémantique de l’énoncé afin de choisir le bon schéma. Cette analyse et la construction du schéma doivent s’appuyer l’une sur l’autre.

Elle s’inspire d’un matériel éducatif largement répandu depuis les années 1950 : les réglettes Cuisenaire. Ces réglettes peuvent être mises en relation soit en les mettant bout à bout (on en addition les longueurs), soit en les mettant côte à côte  (on en compare les longueurs pour chercher la différence).

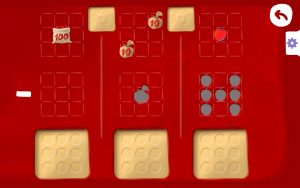
Ici, ces réglettes sont nommés “Les Noums”. Ils peuvent revêtir deux formes:

-dans l’une, les Noums avec les coins arrondis peuvent être scindés (décomposition) ou assemblés (recomposition);

-dans l’autre, les Noums “rectangulaires” ne peuvent être que juxtaposés soit bout à bout (addition), soit bord à bord (soustraction). Ce sont ceux dont l’usage est privilégié lors des activités de modélisation pour résoudre des problèmes.

La solution “Les Noums CP” met à disposition de nombreux outils :

-l’outil “radiographie” qui se veut comme une solution au principal reproche qui a été fait, avec raison, au matériel originel. Avec ce matériel, la réglette 4 n’apparaissait pas formée de 4 unités, elle avait seulement une longueur de 4 unités. A noter que la radiographie peut faire apparaître des Noums unités, des fruits, des habits, des enfants, etc…

-le “Noum inconnu” dont on peut modifier la longueur à loisir qui permet d’engendrer les deux schémas de base, celui de l’addition (les « Noums données » sont mis bout à bout) et celui de la soustraction (ils sont juxtaposés).

-de nombreux laboratoires tels que “la boîte 100”, “la machine de change”, “les opérations posées”, “la machine de multiplication”, “la grille de nombres”, “l’horloge”, etc… Ces applications peuvent très bien servir à l’enseignant en vidéoprojection interactive et sont déjà d’une grande plus-value pédagogique à elles seules.

Tout d’abord, il s’agit de consulter les cinq vidéos de présentation de la méthode pour en appréhender les grands principes.

Comment engager les élèves dans la méthode au travers de la vidéo Les Noums contre Osgard

Il s’agit d’une méthode complète. Pas besoin d’un autre fichier que celui fourni avec l’application. Néanmoins, il est tout à fait possible d’utiliser les outils numériques qu’elle contient dans le cadre d’une autre méthode.

La durée d’une séquence est d’une heure par jour environ : “numérique-collectif” puis “numérique-individuel” puis exercices d’application (un fichier est disponible).

Explicitation de la démarche en classe par Rémi Brissiaud :

1) Dans une classe composée d’élèves de CP uniquement, il est possible d’utiliser une tablette pour deux. Pendant que la moitié des élèves travaille sur les tablettes, l’autre travaille sur le fichier, puis c’est l’inverse. Il faut prévoir des activités complémentaires pour ceux qui sont sur papier (pas d’inquiétude si ceux qui sont sur tablettes ont fini avant, ils ont de quoi s’occuper dans le logiciel). Ça semble aisément gérable pour une classe de CP dédoublé.

2) En cas de classe à deux, voire trois niveaux, il faut craindre que l’attention des non-CP soit irrépressiblement attirée par ce qui se passe lors du “numérique-collectif” (15-20 min). Ce n’est pas trop gênant lorsqu’il s’agit de GS, mais lorsqu’il s’agit de CE1 ou de CE2, cela peut l’être un peu plus. Cette solution pédagogique est très ludique, l’engagement des enfants est grand et est susceptible de développer de la frustration chez les élèves des autres niveaux. Il semble évident que, dans ce cas, il faut avoir autant de tablettes qu’il y a d’élèves de CP et, même, avoir la possibilité de mettre les autres élèves sur un travail sur écran (VPI, ENI)..

3) La solution est installable et fonctionnel sous Android, Ios, Windows phone, Windows, Mac os. Elle ne nécessite pas l’utilisation d’Internet et donc pas wifi qui est encore parfois de mauvaise qualité et dans les écoles. L’usage de la solution est très facile. Pour chaque séquence, une vidéo de 7 min environ propose un exemple d’animation de la séquence. Les enseignants ont été unanimes à considérer que cela rend l’usage de cette ressource très simple et non-chronophage.

Les types d’exercices proposés au cours des séances :

-Les roses sont des laboratoires (icône fiole de laboratoire). Ils permettent de tâtonner, éprouver, tester…

-Les verts sont des défis à réaliser en autonomie (icône ampoule) avec procédure de validation, d’étayage, de rétroaction. La réponse de l’enfant est codée et comparée à ce qu’on lui avait présenté au préalable. Si l’élève fait une erreur, on laisse le temps à l’élève de comprendre son erreur.

Méthode vous permettant de télécharger puis installer l’application / le logiciel Dragon Box

Suivez le protocole ci-dessous à la lettre :

-Rendez-vous sur https://teacher.dragonbox.com/demo_fr?locale=fr et créez-vous un compte enseignant. Un courriel d’activation vous sera envoyé. Il vous faut le consulter et cliquer sur le lien “Confirm your account”. 

–Connectez-vous ensuite avec votre compte à https://teacher.dragonbox.com/users/sign_in?locale=fr.

-Cliquez sur “Tableau de bord“ situé en haut de page vous aurez accès aux programmes d’installation des versions PC et Mac.

Lors de son installation, je vous conseille de choisir la résolution maximale et de décocher “Windowed” afin de pouvoir afficher le programme en plein écran.

Pour les versions Android et Apple, voir ci-dessous.

-Veuillez noter que les ressources citées dans la page de votre compte n’y sont pas disponibles.

Pour les récupérer, accédez tout simplement au dossier en ligne.

Vous y trouverez :

-les affichages des 10 premiers Noums (dossier “PDFaffichages ou à projeter”)

-le manuel/fichier des élèves décliné jusqu’à la période 5 (dossier “PDF fichier”)

-les vidéos explicatives des 88 premières “séquences” commentées par Rémi Brissiaud en personne.

–Créez votre “Fastcode”. Ce code vous permettra, après avoir installé une des versions du logiciels “Les Noums CP” d’activer votre licence d’utilisation.

Veuillez noter que lors de cette activation, vous aurez besoin d’une connexion Internet.

En classe, nul besoin de connexion, l’application est utilisable hors-ligne.

-Pour installer l’application sur tablette, recherchez “Les Noums CP” dans l’outil de recherche du magasin d’application de votre tablette (Play Store ou Apple Store).

Il s’agit ensuite de télécharger l’application “Login Access : Les Noums – CP“.

–Ouvrez l’application sur la tablette,

-Cliquez sur “Connexion“, une page web s’ouvre.

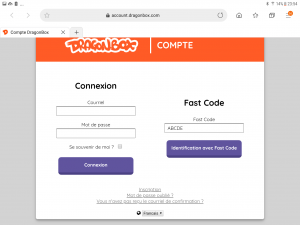
-Authentifiez-vous, c’est là que le Fastcode vous sera utile ! Cela vous évitera de compléter les plages “Courriel” et “Mot de passe”. Autant gagner du temps. Inscrivez-donc le Fastcode dans la zone de saisie correspondante (voir capture ci-dessus).

-La jonction entre votre compte et l’application est réalisée :

-Ça y est ! Votre application est activée !

Lors de l’utilisation du logiciel, toute action réalisée par l’enseignant nécessitera le code “24680”.